By

Contents
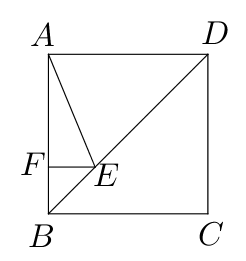
  1. 如图，正方形$ABCD$的边长为4，点$E$在对角线$BD$上，且$\angle
    BAE=22.5^{\circ}$， $EF\bot AB$，垂足为$F$，则$EF$的长为
    ___________ .
  2. 如图，在矩形$ABCD$中，点$E$是$AD$的中点，$\angle EBC$的平分线交$CD$于点
    $F$，将$\triangle DEF$沿$EF$折叠，点$D$恰好落在$BE$上的$M$点处，延长$BC, EF$交于点
    $N$。则下列结论中正确的有（写序号）___________.
    (1) $DF=CF$;
    (2) $BF\bot EN$;
    (3) $\triangle BEN$是等边三角形;
    (4) $\triangle BEF$的面积是$\triangle DEF$面积的3倍.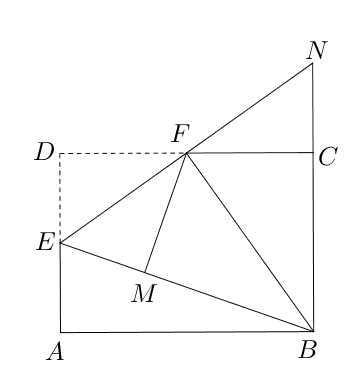
  3. 正方形$ABCD$的边长是4，点$P$是$AD$边的中点，点$E$是正方形边上一点，若
    $\triangle PBE$是等腰三角形，则腰长为___________.
  4. 如图所示，在同一直角坐标系中画出函数$y_1=\dfrac{2}{x}$和函数
    $y_2=\dfrac{x}{2}$的图像，请你根据图像说出当$x$为何值时有
    $\dfrac{2}{x}>\dfrac{x}{2}$.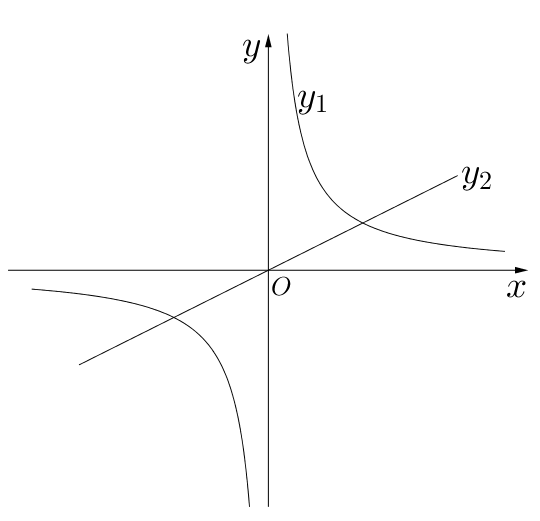
  5. 已知正方形$ABCD$中，$E,F$分别是$BC, CD$上的点，满足$\angle EAF=45^{\circ}$，
    对角线$BD$分别与$AE,AF$交于点$M$和$N$.
    (1) 求证：$EF=BE+DF$;
    (2) 求证：$\angle \alpha=\angle \beta$;
    (3) 求证：$BM^2+DN^2=MN^2$;
    (4) 若正方形边长为6，$F$为$DC$中点，试求$\triangle AEF$的面积$S_{\triangle AEF}$.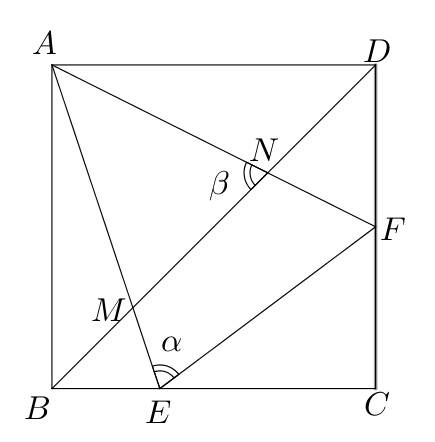
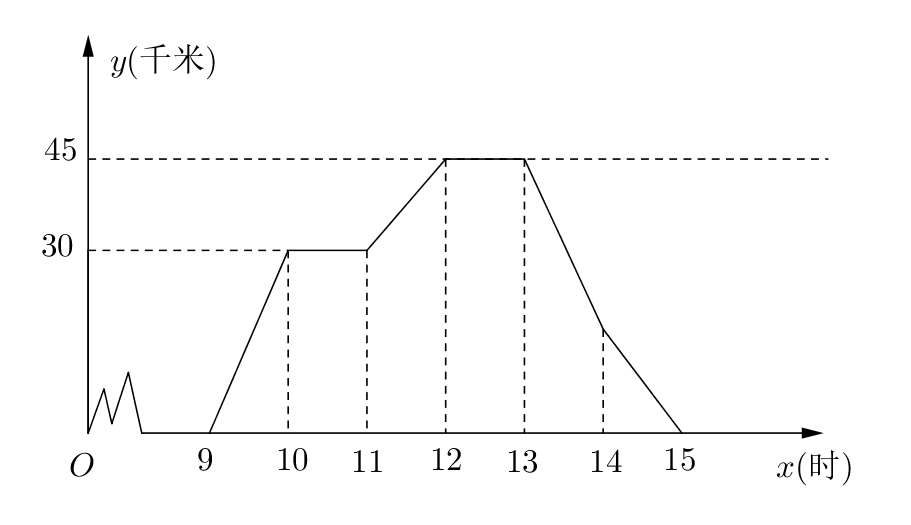
  6. 已知$A,B$两地相距45千米，图中折线表示某骑车人离$A$地的距离$y$与时间
    $x$的函数关系。有一辆客车9点从$B$地出发，以45千米/时的速度匀速行驶，并往返于
    $A,B$两地之间。（乘客上，下车停留时间忽略不计）
    (1) 从折线图可以看出，骑车人一共休息了_______ 次，共休息 ________ 小时；
    (2) 请在图中画出9点至15点之间客车与$A$地的距离$y$随时间$x$变化的函数图像；
    (3) 通过图像观察，骑车人与客车相遇了几交？
Contents