By

Contents
  1. 菱形$ABCD$的周长为8cm，$\angle BAD=120^{\circ}$，则四边形$ABCD$的面积= ___________ .
  2. 如图，四边形$ABCD$为矩形，把纸片$ABCD$沿$AF$折叠，使点$B$恰好落在$CD$的中点
    $E$处，若$CD=6$，则$AF=$ ___________.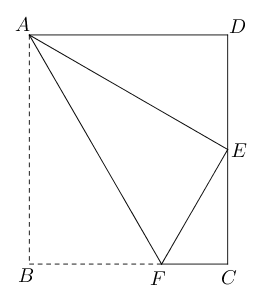
  3. 已知平行四边形$ABCD$，$AE\bot BC$于$E$，$AF\bot DC$于$F$，若$AE=4$，$AF=6$，
    且四边形$ABCD$周长为40，则四边形$ABCD$的面积= ___________.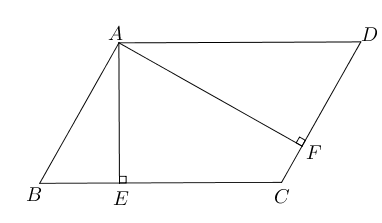
  4. 已知在平行四边形中，$E,F$分别为$AB,CD$的中点，$BD$是对角线，$AG\parallel DB$
    交$CB$延长线于$G$. 若四边形$BEDF$是菱形，则四边形$AGBD$是什么特殊四边形，证明
    你的结论。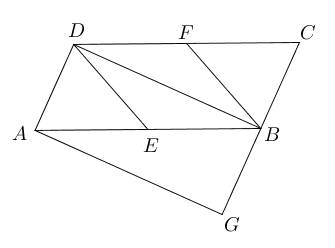
  5. 已知矩形$ABCD$，$E,F$分别为$AB,CD$的中点，将矩形沿$BM$折叠，使点$A$落在$EF$的
    点$N$处，求$\angle ABM$的大小。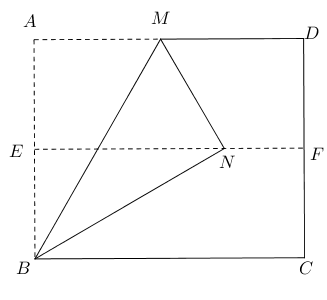
  6. 已知正方形$ABCD$，$E$为$DC$上一动点，过点$E$作$DB$的平行线交$BC$于$F$，延长$AB$至
    $G$使$AB=BG$，连结$GF$交$AE$于点$H$，求证：$DA=HB$.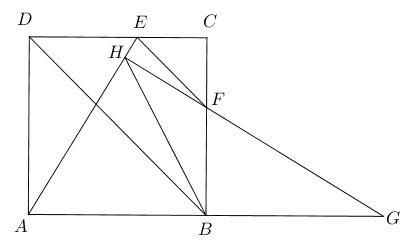
  7. 已知平行四边形$ABCD$，$E,F$分别为$AD,AB$上的点，且$BE=DF$，它们相交于点$O$.
    求证：$CO$平分$\angle DOB$.
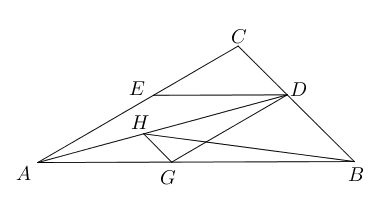
  8. 如图所示，$\triangle ABC$中，$\angle CAB=30^{\circ},\angle CBA=45^{\circ}$,
    $AD$平分$\angle CAB$, 过点$D$分别作$AB,AC$的平行线与$AC,AB$分别交于点$E$和
    $G$,点$H$为线段$AD$上任一点， 如果$DE=2\sqrt{10}$，试求$HG+HB$的最小值。
Contents