By

Contents
  1. 已知四边形$ABCD$为正方形，三角形$CDE$为正三角形，$BE$与$AC$相交于点$F$，
    求证 ：$FA=FE$。
  2. 已知正方形$ABCD$, $M$为$AB$ 上任一点，过点$M$作 $DM$的垂线与$\angle CBE$的平分
    线相交于点$N$，证明：$MD=MN$.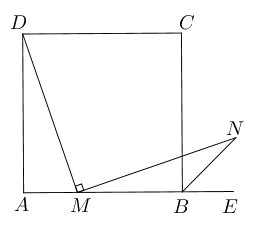
  3. 已知$\angle MON=90^{\circ}$, $OADC$为其内一正方形，$B_1$为线段$ON$上一个动点
    ，使得$AB_1C_1D_1$亦为正方形，在$B_1$运动过程中，请问$\angle C_1CN$是否为定值
    ？请说明理由.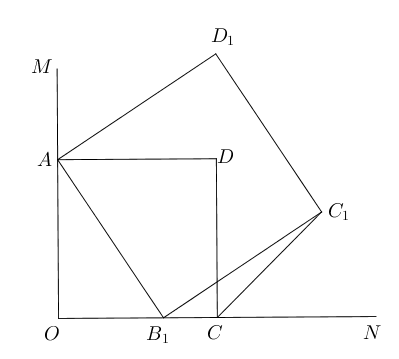
  4. 已知正方形$ABCD$, $BF\parallel AC$且$CA=CF$, 证明$\angle ACF=5\angle F$.
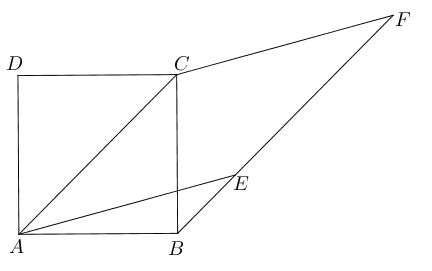
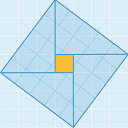
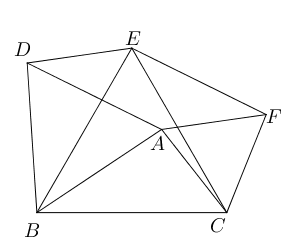
  5. 如图所示，已知三角形$\triangle BDA,\triangle BEC,\triangle FAC$均为正三角形
    1. 证明四边形$DAFE$为平行四边形；
    2. 当$\triangle ABC$满足什么条件时，$DAFE$不构成四边形；
    3. 当$\triangle ABC$满足什么条件时，$DAFE$为菱形；
    4. 当$\triangle ABC$满足什么条件时，$DAEF$为矩形。
  6. 如图所示，已知$\triangle ABE$和$\triangle ACF$都为等腰直角三角形，$M$为$BC$中
    点，求证：$\triangle EFM$为等腰直角三角形。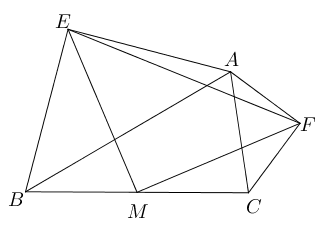
  7. 如图所示，已知正方形$ABCD$，$M,N$分别是$AD,DC$的中点，$CM$和$BN$相交于点
    $P$，求证：$AP=AB$.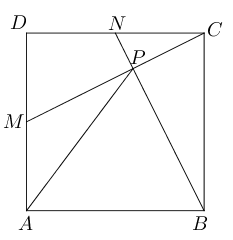
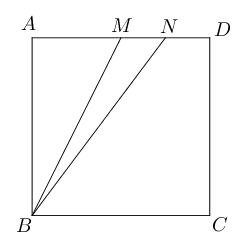
  8. 如图所示，已知正方形$ABCD$，$M$为$AD$中点，$N$为$MD$上一点，满足$BN=ND+DC$.
    证明：$\angle CBN=2\angle ABM$.
Contents