By

Contents
  1. 如图所示，矩形$ABCD$中，$AB=5,AD=12$,$P$为$AD$上一动点（不包括端点），过
    $P$分别作$BD,AC$的垂线，垂足分别为$E,F$, 试求$PE+PF$.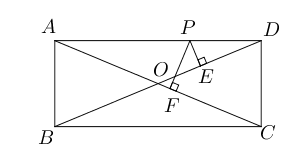
  2. 如图所示，$O$为$AC$边上一动点，$MN$过点$O$且平行于$BC$, $\angle ACB$和$\angle ACD$
    的平分线分别与$MN$交于点$E$和$F$，请问：在$O$运动过程中，四边形$AECF$可能是矩形吗？请说明理由。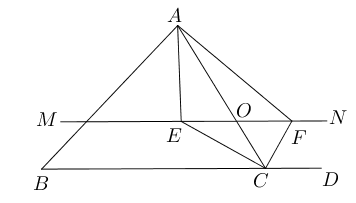
  3. 如图所示，直角三角形$ABC$中，$\angle ACB=90^{\circ}$, $CD\bot AB$,$M$为$AB$中
    点，求证：$\angle \alpha=\angle\beta$.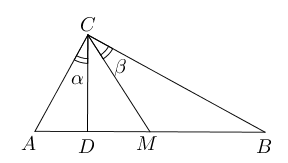
  4. 如图所示，已经矩形$ABCD$, 过点$C$作$BD$的垂线与$\angle BAD$的平分线交于点
    $F$，求证：$CA=CF$.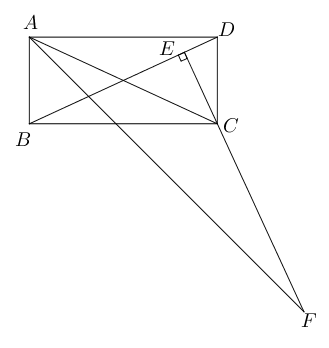
  5. 如图所示，在直角三角形$ABC$中，$\angle BAC=90^{\circ}$, $AD\bot BC$, $\angle
    ABC$的平分线
    分别交$AD,AC$于$E,F$，过点$E$作$EG\parallel BC$交$AC$于$G$. 求证 ：$AF=GC$.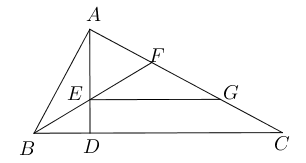
  6. 如图所示，已知平行四边形$ABCD$, $DE\bot AB$, $MB=MC=CD$,
    求证：$\angle EMC=3\angle BEM$.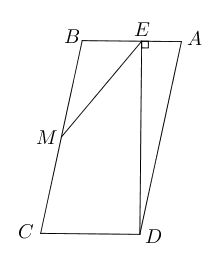
  7. (选做)如图所示，$P$为矩形$ABCD$内一点，$\triangle ABP$和$\triangle PBC$的面积分别是
    5和13，求$\triangle PBD$的面积.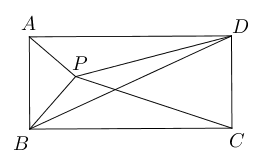
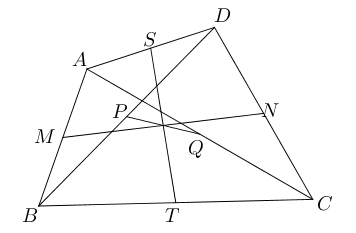
  8. (选做) 如图所示，四边形$ABCD$中，$M,T,N,S,P,Q$分别是$AB,BC,CD,DA,BD,AC$的中点
    ，证明：$MN,ST,PQ$三线交于一点。
Contents