By

Contents
  1. 计算$(\sqrt 3-2)^{2017}\cdot (\sqrt 3+2)^{2016}=$ ___________.
  2. 已知$x=\dfrac{\sqrt 3-1}{\sqrt 3+1},y=\dfrac{\sqrt 3+1}{\sqrt 3-1}$, 则
    $x^4+y^4=$ ___________.
  3. 设$x<0,y<0$, 请化简: $x\sqrt{\dfrac{y}{x}}-\dfrac{1}{y}\sqrt{xy^3}-\sqrt{x^3y}$ =___________.
  4. 如下图所示四边形$ABCD$中，$AB=3,BC=12,CD=13,DA=4$, 且$DA\bot AB$, 则四边形
    $ABCD$的面积是___________.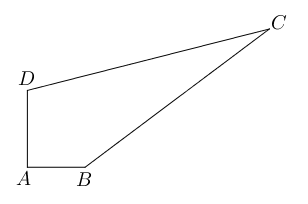
  5. 如图，线段$AB,CD$相交于点$O$，且图上各点把线段$AB,CD$四等分，则这些点可以构成
    _________个平行四边形.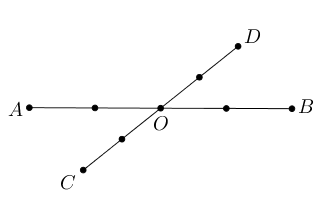
  6. 如图所示，已知$AB\parallel CD$, 请添加一个条件使$ABCD$为平行四边形，请用至少
    三种不同方法：1___________;2___________; 3___________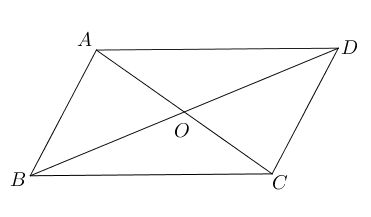
  7. 下面几句话中正确的有___________
    1. 一组对边相等且一组对角相等的四边形是平行四边形.
    2. 一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形.
    3. 两组对角分别相等的四边形是平行四边形.
    4. 一组对角相等且连结这一组对角顶点的对角线被另一条对角线所平分的四边形是平行
      四边形.
    5. 一组对边平行，另一组对边相等的四边形是平行四边形.
  8. 如图，在$\triangle ABC$中，$\angle ABC=90^{\circ}$, $\angle BAC=60^{\circ}, \triangle ACD$ 是等边三角形，
    $E$是$AC$的中点，连接$BE$并延长，交$DC$于点$F$，求证
    1. $\triangle ABE$全等于$\triangle CFE$.
    2. 四边形$ABFD$是平行四边形。
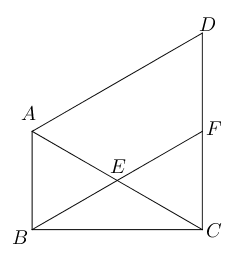
  9. 如图，$\triangle ABC$中，$M$是$BC$的中点，$AD$是$\angle A$的平分线，
    $BD\bot AD$于$D$，$AB=12, AC=18$, 求$DM$的长.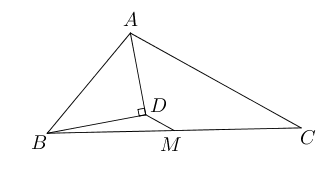
  10. 证明平行四边形对角线的平方和等于四条边的平方之和。
  11. （选做）$\triangle ABC$中，以$AB$，$AC$为边分别向外作等边三角形$\triangle ABD$与
    $\triangle ACE$, $M$为$AD$中点，$N$为$AE$中点，$P$为$BC$中点，$Q$为$MN$的中点
    ，连接$PQ$， 求证：$PQ\bot MN$.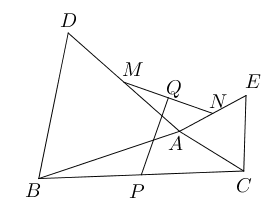
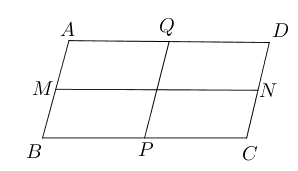
  12. （选做）四边形$ABCD$中，$AB,BC,CD,DA$的中点分别为$M,P,N,Q$且
    $MN+PQ=\dfrac{1}{2}(AB+BC+CD+DA)$, 求证：四边形$ABCD$是平行四边形。
Contents