二次根式及勾股定理和平行四边形部分题目

1. 已知$a>0$化简$\sqrt{\dfrac{-4a}{b}}=$ ___________.
2. 已知$a-b=2\sqrt3-1, ab=\sqrt3$则$(a+1)(b-1)=$ ___________.
3. 三角形的一边长是$\sqrt{60}$cm, 该边上的高是$\sqrt{30}$cm，则该三角形的面积
   =___________.
4. 若直角三角形的两边长分别为5和12，则第三边长为 ___________.
5. 在$\triangle ABC$中，$AB=10, AC=2\sqrt{10}$,$BC$边上的高$AD=6$，则另一边
   $BC=$ ___________.
6. 如图，在平行四边形$ABCD$中，$BE$平分$\angle ABC$, $AB=3, DE=2$, 则$ABCD$的周
   长为 ___________.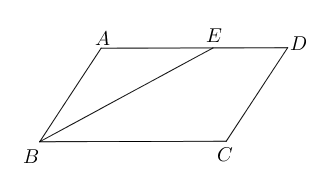
   
7. 如图，平行四边形$ABCD$中，$AC=6, BD=10, AD=a$, 则$a$的取值范围是
   ___________.
   
8. 如图，在平行四边形$ABCD$中，$E$为$BC$边上一点，且$AB=AE$.
   证明：$\triangle ABC$全等于$\triangle EAD$.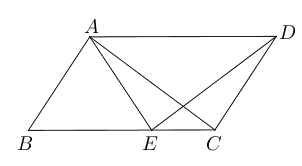
   
9. 已知$a>0,b>0$且$\sqrt a(\sqrt a+\sqrt b)=3\sqrt b(\sqrt a+5\sqrt b)$, 求
   $$
   \dfrac{2a+3b+\sqrt{ab}}{a-b+\sqrt{ab}}
   $$的值。
10. 在$\triangle ABC$中，$\angle A=60^{\circ},\angle C=90^{\circ}$,
    $BC=3+2\sqrt3$, $BD$平分$\angle ABC$交$AC$于$D$。求$AD$.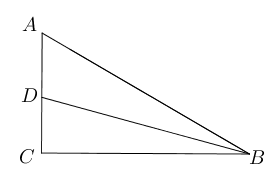
    
11. 点$E,F$分别为正方形$ABCD$边$BC, CD$上的点，$BE=CE, \angle EAF=45^{\circ}$, 如
    果$AB=6$, 试求$\triangle AEF$的面积。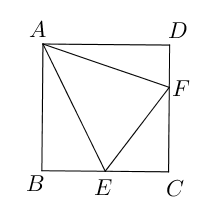
    
12. 广州某小区有一块直角三角形的公共绿地，量得两直角边长分别为12m和16m，现在要将
    绿地扩充成等腰三角形状，且扩充部分是以16m为直角边的直角三角形，求扩充后等腰三
    角形绿地的周长。