By

Contents
  1. 1. 二次根式运算及勾股定理

二次根式运算及勾股定理

  1. 计算$2\div(\sqrt2-1)$=___________
  2. 已知实数$a$满足$|2017-a|+\sqrt{a-2018}=a$, 则
    $a-2017^2$=___________
  3. 边长为$4$的正三角形面积=___________
  4. 已知$A(-2,1), B(3,4)$, 则$AB$之间的距离$|AB|$=___________
  5. 化简$\sqrt{7+4\sqrt 3}$= ___________
  6. 已知一直角三角形两直角边分别为5和12，则这个三角形斜边上的高为
    ___________
  7. 在$\triangle ABC$中，$AB=15,AC=13$,高$AD=12$, 则$\triangle ABC$周长是
    ___________
  8. 计算($m>0,n>0$)
    $$
    \dfrac{n}{m}\sqrt{\dfrac{m}{2n^3}}\cdot \left(-\dfrac{1}{m}\sqrt{\dfrac{n^3}{m^3}}\right) \div \sqrt{\dfrac{n}{2m^3}}
    $$
  9. 已知：如图所示$\angle B=\angle D=90^{\circ},\angle A=60^{\circ},AB=4, CD=2$.
    求：四边形$ABCD$的面积。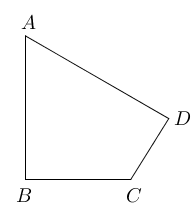
  10. 如图，在平面直角坐标系中，矩形$OABC$的顶点$A,C$的坐标分别为$(10,0),(0,4)$, 点
    $D$是$OA$的中点，点$P$在$BC$上运动，当$\triangle ODP$是等腰三角形时，求$P$的
    坐标。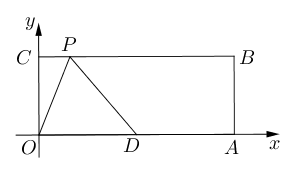
  11. 如下图所示，由六个单元格组成的图形，图中的$\angle \alpha+\angle\beta$为多少度
    ?说明理由。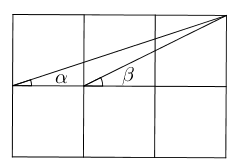
  12. 如图，是一块长、宽、高分别是4cm、2cm和1cm 的长方体木块，一只蚂蚁要从长方体木
    块的一个顶点$A$处，沿着长方体的表面到长方体上和$A$相对的顶点$B$处吃食物，那么
    它需要爬行的最短路径是多少？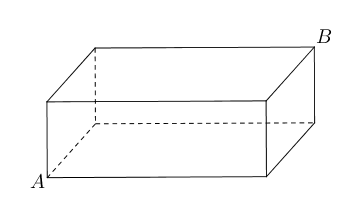
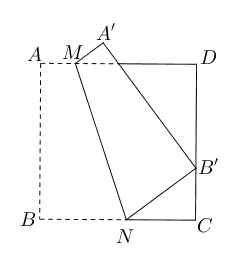
  13. 如下图所示，四边形$ABCD$是边长为9的正方形纸片，将其沿$MN$折叠，使点$B$落在边
    $CD$上的$B’$处，点$A$对应点为$A’$，且$B’C=3$, 则求：
    1. $BN$的长度；
    2. $AM$的长度。
  14. 如图，已知$\triangle ABC$为正三角形，$P$为其内一点，满足$PA=3,PB=4,PC=5$
    1. 求$\angle APB$的大小。
    2. （选做）求边长$AB$的大小。
Contents
  1. 1. 二次根式运算及勾股定理