1. 一次函数的图像过$(3,0)$, 且与坐标轴围成的面积为9，求一次函数的函数关系式。
2. 设直线$nx+(n+1)y=\sqrt{2}\ (n$为自然数)与坐标轴围成的三角形面积为
   $S_n\ (n=1,2,\ldots, 2017)$, 试求$S_1+S_2+\cdots+S_{2017}$的值。
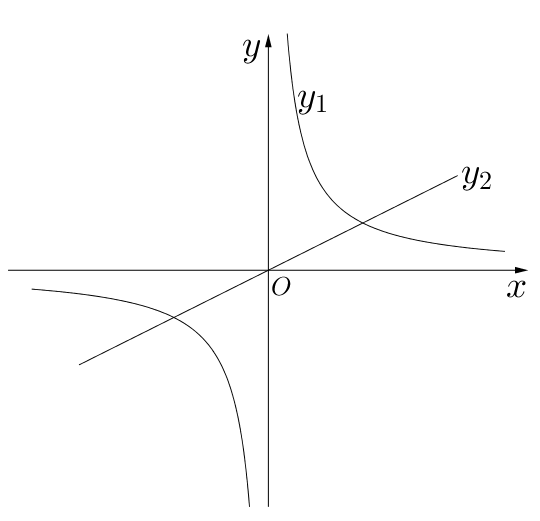
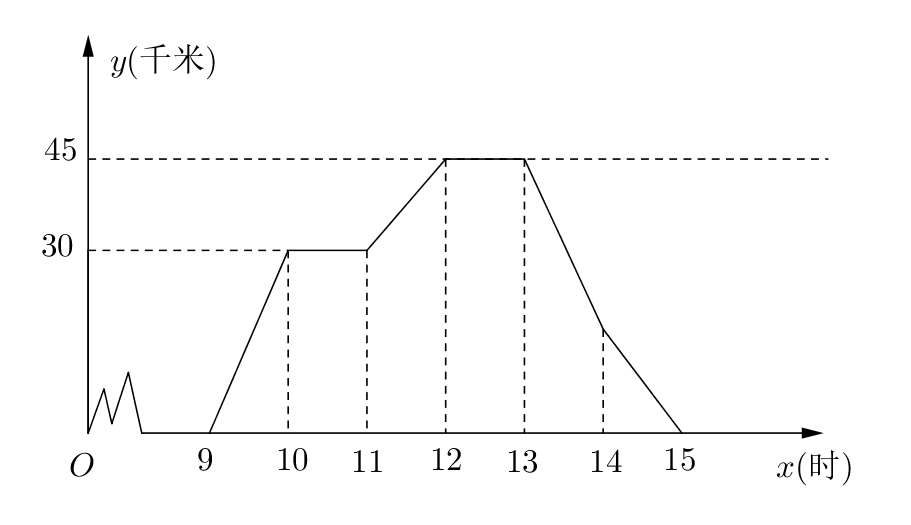
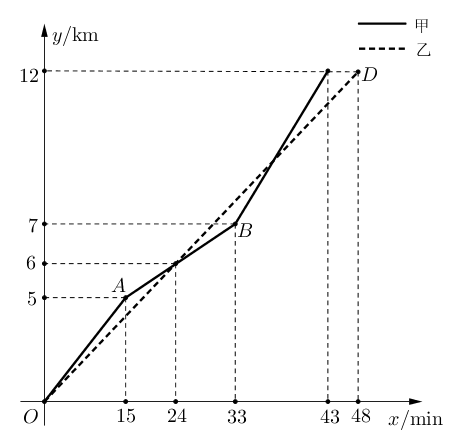
3. 如图所表示甲、乙两名选手在一次自行车越野赛中，路程$y$(km)随时间$x$(min)变化的
   图像（全程），根据图像回答下列问题：
   （1）求比赛开始多少分钟时，两人第一次相遇；
   （2）求这次比赛的全成是多少千米；
   （3）求比赛开始多少分钟时，两人第二次相遇。
   
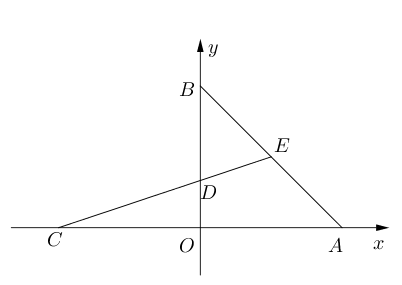
4. 已知：如图，平面直角坐标系中，$A(1,0),B(0,1),C(-1,0)$, 过点$C$的直线，交
   $y$轴于点$D$, 交线段$AB$于点$E$.
   (1)求直线$AB$的解析式；
   (2)若$\triangle OCD$与$\triangle BDE$的面积相等，求直线$CE$的解析式。
   

1. 如图，正方形$ABCD$的边长为4，点$E$在对角线$BD$上，且$\angle
   BAE=22.5^{\circ}$， $EF\bot AB$，垂足为$F$，则$EF$的长为
   ___________ .
   
2. 如图，在矩形$ABCD$中，点$E$是$AD$的中点，$\angle EBC$的平分线交$CD$于点
   $F$，将$\triangle DEF$沿$EF$折叠，点$D$恰好落在$BE$上的$M$点处，延长$BC, EF$交于点
   $N$。则下列结论中正确的有（写序号）___________.
   (1) $DF=CF$;
   (2) $BF\bot EN$;
   (3) $\triangle BEN$是等边三角形;
   (4) $\triangle BEF$的面积是$\triangle DEF$面积的3倍.
   
3. 正方形$ABCD$的边长是4，点$P$是$AD$边的中点，点$E$是正方形边上一点，若
   $\triangle PBE$是等腰三角形，则腰长为___________.
4. 如图所示，在同一直角坐标系中画出函数$y_1=\dfrac{2}{x}$和函数
   $y_2=\dfrac{x}{2}$的图像，请你根据图像说出当$x$为何值时有
   $\dfrac{2}{x}>\dfrac{x}{2}$.
   
5. 已知正方形$ABCD$中，$E,F$分别是$BC, CD$上的点，满足$\angle EAF=45^{\circ}$，
   对角线$BD$分别与$AE,AF$交于点$M$和$N$.
   (1) 求证：$EF=BE+DF$;
   (2) 求证：$\angle \alpha=\angle \beta$;
   (3) 求证：$BM^2+DN^2=MN^2$;
   (4) 若正方形边长为6，$F$为$DC$中点，试求$\triangle AEF$的面积$S_{\triangle AEF}$.
   
6. 已知$A,B$两地相距45千米，图中折线表示某骑车人离$A$地的距离$y$与时间
   $x$的函数关系。有一辆客车9点从$B$地出发，以45千米/时的速度匀速行驶，并往返于
   $A,B$两地之间。（乘客上，下车停留时间忽略不计）
   (1) 从折线图可以看出，骑车人一共休息了_______ 次，共休息 ________ 小时；
   (2) 请在图中画出9点至15点之间客车与$A$地的距离$y$随时间$x$变化的函数图像；
   (3) 通过图像观察，骑车人与客车相遇了几交？
   

1. 菱形$ABCD$的周长为8cm，$\angle BAD=120^{\circ}$，则四边形$ABCD$的面积= ___________ .
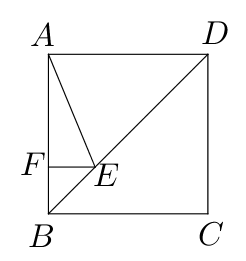
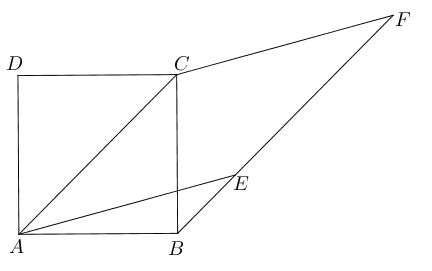
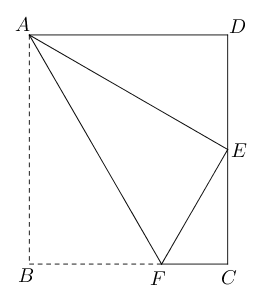
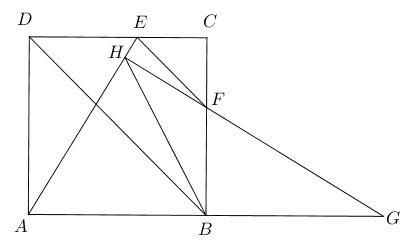
2. 如图，四边形$ABCD$为矩形，把纸片$ABCD$沿$AF$折叠，使点$B$恰好落在$CD$的中点
   $E$处，若$CD=6$，则$AF=$ ___________.
   
3. 已知平行四边形$ABCD$，$AE\bot BC$于$E$，$AF\bot DC$于$F$，若$AE=4$，$AF=6$，
   且四边形$ABCD$周长为40，则四边形$ABCD$的面积= ___________.
   
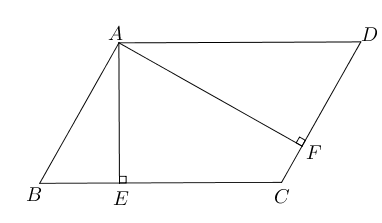
4. 已知在平行四边形中，$E,F$分别为$AB,CD$的中点，$BD$是对角线，$AG\parallel DB$
   交$CB$延长线于$G$. 若四边形$BEDF$是菱形，则四边形$AGBD$是什么特殊四边形，证明
   你的结论。
   
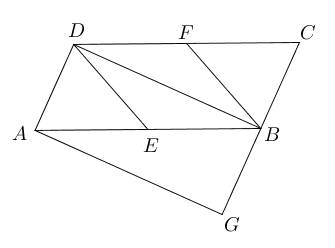
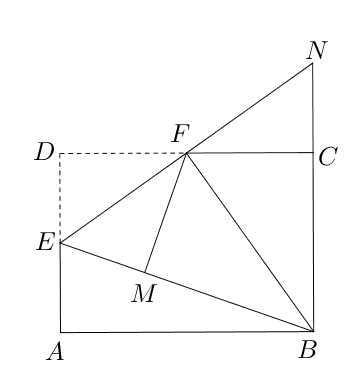
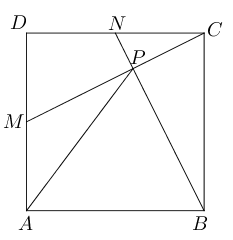
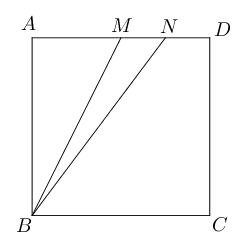
5. 已知矩形$ABCD$，$E,F$分别为$AB,CD$的中点，将矩形沿$BM$折叠，使点$A$落在$EF$的
   点$N$处，求$\angle ABM$的大小。
   
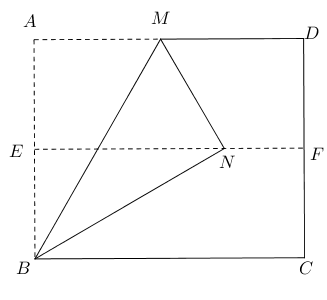
6. 已知正方形$ABCD$，$E$为$DC$上一动点，过点$E$作$DB$的平行线交$BC$于$F$，延长$AB$至
   $G$使$AB=BG$，连结$GF$交$AE$于点$H$，求证：$DA=HB$.
   
7. 已知平行四边形$ABCD$，$E,F$分别为$AD,AB$上的点，且$BE=DF$，它们相交于点$O$.
   求证：$CO$平分$\angle DOB$.
   
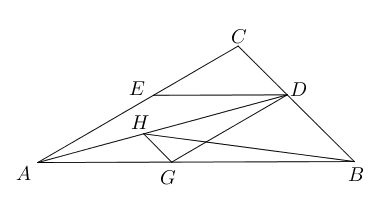
8. 如图所示，$\triangle ABC$中，$\angle CAB=30^{\circ},\angle CBA=45^{\circ}$,
   $AD$平分$\angle CAB$, 过点$D$分别作$AB,AC$的平行线与$AC,AB$分别交于点$E$和
   $G$,点$H$为线段$AD$上任一点， 如果$DE=2\sqrt{10}$，试求$HG+HB$的最小值。
   

1. 已知四边形$ABCD$为正方形，三角形$CDE$为正三角形，$BE$与$AC$相交于点$F$，
   求证 ：$FA=FE$。
   
2. 已知正方形$ABCD$, $M$为$AB$ 上任一点，过点$M$作 $DM$的垂线与$\angle CBE$的平分
   线相交于点$N$，证明：$MD=MN$.
   
3. 已知$\angle MON=90^{\circ}$, $OADC$为其内一正方形，$B_1$为线段$ON$上一个动点
   ，使得$AB_1C_1D_1$亦为正方形，在$B_1$运动过程中，请问$\angle C_1CN$是否为定值
   ？请说明理由.
   
4. 已知正方形$ABCD$, $BF\parallel AC$且$CA=CF$, 证明$\angle ACF=5\angle F$.
   
5. 如图所示，已知三角形$\triangle BDA,\triangle BEC,\triangle FAC$均为正三角形
   1. 证明四边形$DAFE$为平行四边形；
   2. 当$\triangle ABC$满足什么条件时，$DAFE$不构成四边形；
   3. 当$\triangle ABC$满足什么条件时，$DAFE$为菱形；
   4. 当$\triangle ABC$满足什么条件时，$DAEF$为矩形。
      
6. 如图所示，已知$\triangle ABE$和$\triangle ACF$都为等腰直角三角形，$M$为$BC$中
   点，求证：$\triangle EFM$为等腰直角三角形。
   
7. 如图所示，已知正方形$ABCD$，$M,N$分别是$AD,DC$的中点，$CM$和$BN$相交于点
   $P$，求证：$AP=AB$.
   
8. 如图所示，已知正方形$ABCD$，$M$为$AD$中点，$N$为$MD$上一点，满足$BN=ND+DC$.
   证明：$\angle CBN=2\angle ABM$.
   

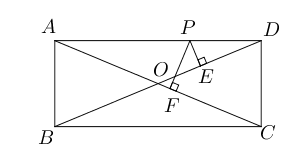
1. 如图所示，矩形$ABCD$中，$AB=5,AD=12$,$P$为$AD$上一动点（不包括端点），过
   $P$分别作$BD,AC$的垂线，垂足分别为$E,F$, 试求$PE+PF$.
   
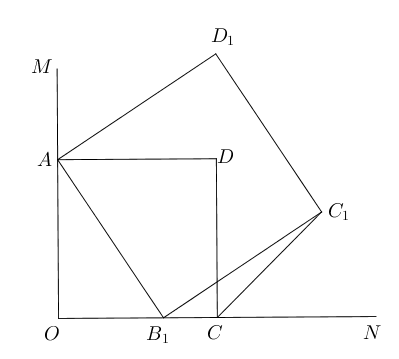
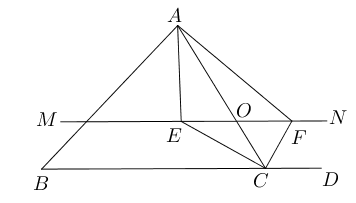
2. 如图所示，$O$为$AC$边上一动点，$MN$过点$O$且平行于$BC$, $\angle ACB$和$\angle ACD$
   的平分线分别与$MN$交于点$E$和$F$，请问：在$O$运动过程中，四边形$AECF$可能是矩形吗？请说明理由。
   
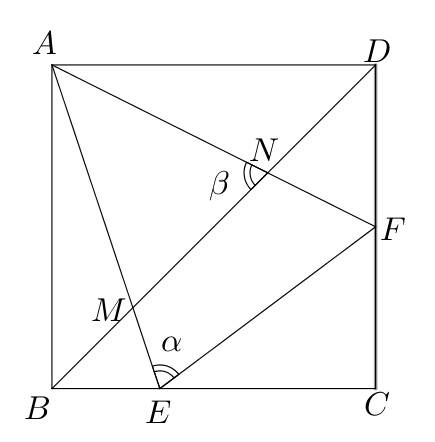
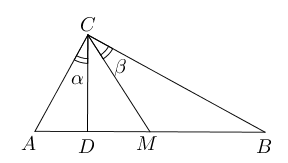
3. 如图所示，直角三角形$ABC$中，$\angle ACB=90^{\circ}$, $CD\bot AB$,$M$为$AB$中
   点，求证：$\angle \alpha=\angle\beta$.
   
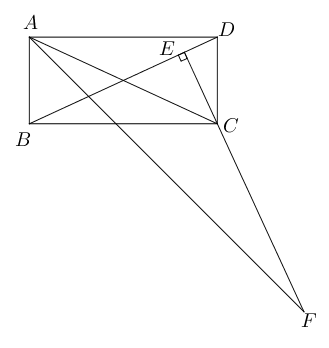
4. 如图所示，已经矩形$ABCD$, 过点$C$作$BD$的垂线与$\angle BAD$的平分线交于点
   $F$，求证：$CA=CF$.
   
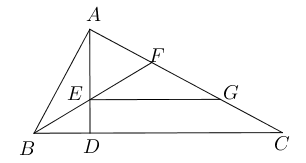
5. 如图所示，在直角三角形$ABC$中，$\angle BAC=90^{\circ}$, $AD\bot BC$, $\angle
   ABC$的平分线
   分别交$AD,AC$于$E,F$，过点$E$作$EG\parallel BC$交$AC$于$G$. 求证 ：$AF=GC$.
   
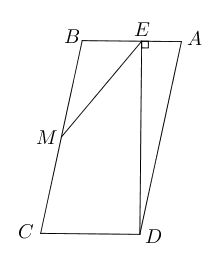
6. 如图所示，已知平行四边形$ABCD$, $DE\bot AB$, $MB=MC=CD$,
   求证：$\angle EMC=3\angle BEM$.
   
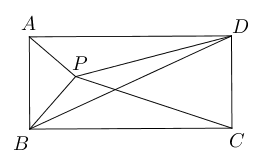
7. (选做)如图所示，$P$为矩形$ABCD$内一点，$\triangle ABP$和$\triangle PBC$的面积分别是
   5和13，求$\triangle PBD$的面积.
   
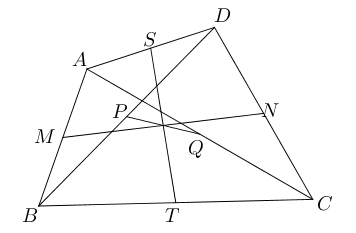
8. (选做) 如图所示，四边形$ABCD$中，$M,T,N,S,P,Q$分别是$AB,BC,CD,DA,BD,AC$的中点
   ，证明：$MN,ST,PQ$三线交于一点。
   

1. 计算$(\sqrt 3-2)^{2017}\cdot (\sqrt 3+2)^{2016}=$ ___________.
2. 已知$x=\dfrac{\sqrt 3-1}{\sqrt 3+1},y=\dfrac{\sqrt 3+1}{\sqrt 3-1}$, 则
   $x^4+y^4=$ ___________.
3. 设$x<0,y<0$, 请化简: $x\sqrt{\dfrac{y}{x}}-\dfrac{1}{y}\sqrt{xy^3}-\sqrt{x^3y}$ =___________.
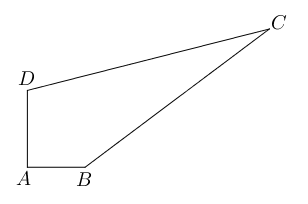
4. 如下图所示四边形$ABCD$中，$AB=3,BC=12,CD=13,DA=4$, 且$DA\bot AB$, 则四边形
   $ABCD$的面积是___________.
   
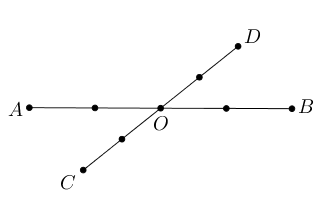
5. 如图，线段$AB,CD$相交于点$O$，且图上各点把线段$AB,CD$四等分，则这些点可以构成
   _________个平行四边形.
   
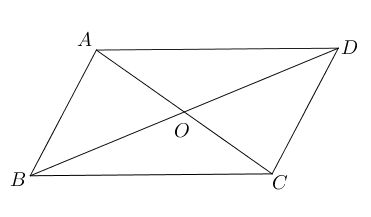
6. 如图所示，已知$AB\parallel CD$, 请添加一个条件使$ABCD$为平行四边形，请用至少
   三种不同方法：1___________;2___________; 3___________
   
7. 下面几句话中正确的有___________
   1. 一组对边相等且一组对角相等的四边形是平行四边形.
   2. 一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形.
   3. 两组对角分别相等的四边形是平行四边形.
   4. 一组对角相等且连结这一组对角顶点的对角线被另一条对角线所平分的四边形是平行
      四边形.
   5. 一组对边平行，另一组对边相等的四边形是平行四边形.
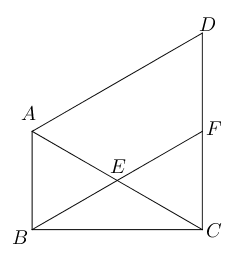
8. 如图，在$\triangle ABC$中，$\angle ABC=90^{\circ}$, $\angle BAC=60^{\circ}, \triangle ACD$ 是等边三角形，
   $E$是$AC$的中点，连接$BE$并延长，交$DC$于点$F$，求证
   1. $\triangle ABE$全等于$\triangle CFE$.
   2. 四边形$ABFD$是平行四边形。
      
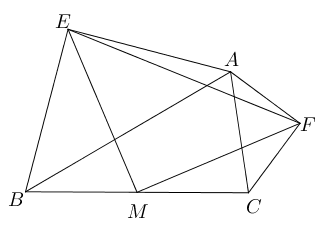
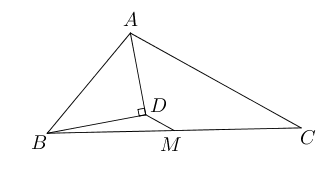
9. 如图，$\triangle ABC$中，$M$是$BC$的中点，$AD$是$\angle A$的平分线，
   $BD\bot AD$于$D$，$AB=12, AC=18$, 求$DM$的长.
   
10. 证明平行四边形对角线的平方和等于四条边的平方之和。
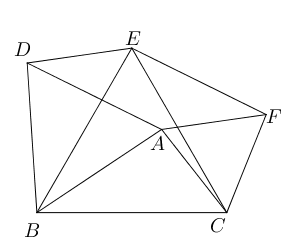
11. （选做）$\triangle ABC$中，以$AB$，$AC$为边分别向外作等边三角形$\triangle ABD$与
    $\triangle ACE$, $M$为$AD$中点，$N$为$AE$中点，$P$为$BC$中点，$Q$为$MN$的中点
    ，连接$PQ$， 求证：$PQ\bot MN$.
    
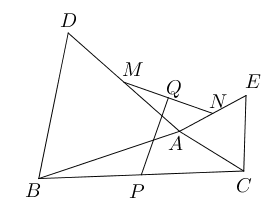
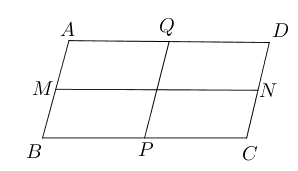
12. （选做）四边形$ABCD$中，$AB,BC,CD,DA$的中点分别为$M,P,N,Q$且
    $MN+PQ=\dfrac{1}{2}(AB+BC+CD+DA)$, 求证：四边形$ABCD$是平行四边形。
    

二次根式及勾股定理和平行四边形部分题目

1. 已知$a>0$化简$\sqrt{\dfrac{-4a}{b}}=$ ___________.
2. 已知$a-b=2\sqrt3-1, ab=\sqrt3$则$(a+1)(b-1)=$ ___________.
3. 三角形的一边长是$\sqrt{60}$cm, 该边上的高是$\sqrt{30}$cm，则该三角形的面积
   =___________.
4. 若直角三角形的两边长分别为5和12，则第三边长为 ___________.
5. 在$\triangle ABC$中，$AB=10, AC=2\sqrt{10}$,$BC$边上的高$AD=6$，则另一边
   $BC=$ ___________.
6. 如图，在平行四边形$ABCD$中，$BE$平分$\angle ABC$, $AB=3, DE=2$, 则$ABCD$的周
   长为 ___________.
   
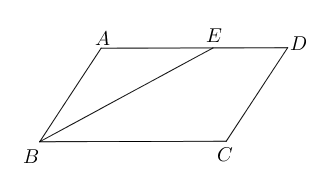
7. 如图，平行四边形$ABCD$中，$AC=6, BD=10, AD=a$, 则$a$的取值范围是
   ___________.
   
8. 如图，在平行四边形$ABCD$中，$E$为$BC$边上一点，且$AB=AE$.
   证明：$\triangle ABC$全等于$\triangle EAD$.
   
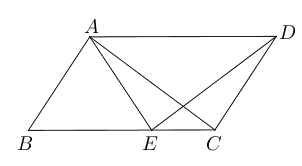
9. 已知$a>0,b>0$且$\sqrt a(\sqrt a+\sqrt b)=3\sqrt b(\sqrt a+5\sqrt b)$, 求
   $$
   \dfrac{2a+3b+\sqrt{ab}}{a-b+\sqrt{ab}}
   $$的值。
10. 在$\triangle ABC$中，$\angle A=60^{\circ},\angle C=90^{\circ}$,
    $BC=3+2\sqrt3$, $BD$平分$\angle ABC$交$AC$于$D$。求$AD$.
    
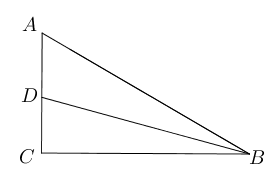
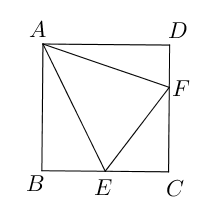
11. 点$E,F$分别为正方形$ABCD$边$BC, CD$上的点，$BE=CE, \angle EAF=45^{\circ}$, 如
    果$AB=6$, 试求$\triangle AEF$的面积。
    
12. 广州某小区有一块直角三角形的公共绿地，量得两直角边长分别为12m和16m，现在要将
    绿地扩充成等腰三角形状，且扩充部分是以16m为直角边的直角三角形，求扩充后等腰三
    角形绿地的周长。

二次根式运算及勾股定理

1. 计算$2\div(\sqrt2-1)$=___________
2. 已知实数$a$满足$|2017-a|+\sqrt{a-2018}=a$, 则
   $a-2017^2$=___________
3. 边长为$4$的正三角形面积=___________
4. 已知$A(-2,1), B(3,4)$, 则$AB$之间的距离$|AB|$=___________
5. 化简$\sqrt{7+4\sqrt 3}$= ___________
6. 已知一直角三角形两直角边分别为5和12，则这个三角形斜边上的高为
   ___________
7. 在$\triangle ABC$中，$AB=15,AC=13$,高$AD=12$, 则$\triangle ABC$周长是
   ___________
8. 计算($m>0,n>0$)
   $$
   \dfrac{n}{m}\sqrt{\dfrac{m}{2n^3}}\cdot \left(-\dfrac{1}{m}\sqrt{\dfrac{n^3}{m^3}}\right) \div \sqrt{\dfrac{n}{2m^3}}
   $$
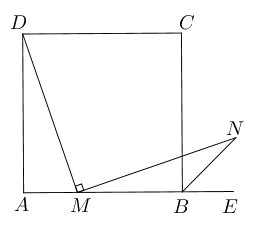
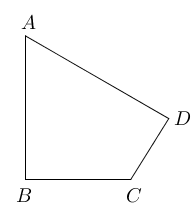
9. 已知：如图所示$\angle B=\angle D=90^{\circ},\angle A=60^{\circ},AB=4, CD=2$.
   求：四边形$ABCD$的面积。
   
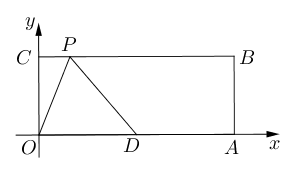
10. 如图，在平面直角坐标系中，矩形$OABC$的顶点$A,C$的坐标分别为$(10,0),(0,4)$, 点
    $D$是$OA$的中点，点$P$在$BC$上运动，当$\triangle ODP$是等腰三角形时，求$P$的
    坐标。
    
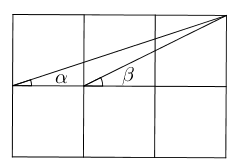
11. 如下图所示，由六个单元格组成的图形，图中的$\angle \alpha+\angle\beta$为多少度
    ?说明理由。
    
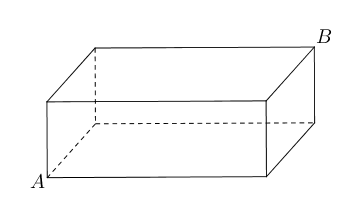
12. 如图，是一块长、宽、高分别是4cm、2cm和1cm 的长方体木块，一只蚂蚁要从长方体木
    块的一个顶点$A$处，沿着长方体的表面到长方体上和$A$相对的顶点$B$处吃食物，那么
    它需要爬行的最短路径是多少？
    
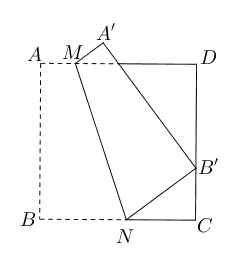
13. 如下图所示，四边形$ABCD$是边长为9的正方形纸片，将其沿$MN$折叠，使点$B$落在边
    $CD$上的$B’$处，点$A$对应点为$A’$，且$B’C=3$, 则求：
    1. $BN$的长度；
    2. $AM$的长度。
       
14. 如图，已知$\triangle ABC$为正三角形，$P$为其内一点，满足$PA=3,PB=4,PC=5$
    1. 求$\angle APB$的大小。
    2. （选做）求边长$AB$的大小。
       

二次根式的加减运算及综合

1. 化简$\sqrt{25\dfrac{1}{4}}$等于_________.
2. 等式$\dfrac{\sqrt x}{\sqrt{1-x}}=\sqrt{\dfrac{x}{1-x}}$成立的条件是
   ________.
3. 计算$(2\sqrt{48}-3\sqrt{72})\div \sqrt6$= _________.
4. 计算$\sqrt{12}\div (\sqrt 3-2\sqrt2)=$ _________.
5. 计算$(\sqrt2+\sqrt3-\sqrt5)(\sqrt2-\sqrt3+\sqrt5)=$ ______.
6. 若$\sqrt{(2a-1)^2}=1-2a$, 则$a$的取值范围是 _________.
7. 化简
   $$
   \sqrt{-a^3}+\sqrt{\dfrac{4a^2}{9b^2}}\ (b<0)
   $$
8. 已知$a+b=4,ab=3$ 求下列式子的值。
   $$
   \sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{b}{a}}
   $$
9. 已知$a=\dfrac{1}{\sqrt3-\sqrt2},b=\dfrac{1}{\sqrt3+\sqrt2}$求值：
   $$
   \dfrac{\sqrt a-\sqrt b}{\sqrt a+\sqrt b}+\left[\dfrac{\sqrt
   a}{a+\sqrt{ab}}-\dfrac{\sqrt b}{b-\sqrt{ab}}\right]\div
   \dfrac{1}{\sqrt b}
   $$
10. 化简
    $$
    \dfrac{\sqrt{x+1}-\sqrt x}{\sqrt{x+1}+\sqrt x}+\dfrac{\sqrt{x+1}+\sqrt x}{\sqrt{x+1}-\sqrt x}
    $$
11. 已知$a=\dfrac{1}{\sqrt 3+\sqrt 2}$求值：
    $$
    \sqrt{\left(a-\dfrac{1}{a}\right)^2+4}-\sqrt{\left(a+\dfrac{1}{a}\right)^2-4}
    $$
12. 已知$x=\sqrt 2-1$ 求值：
    $$
    \dfrac{\sqrt{1+x}}{\sqrt{1+x}+\sqrt{1-x}}+\dfrac{1-x}{\sqrt{1-x^2}-1+x}
    $$

1. 下列哪些不是二次根式：$\sqrt{x-2}$,$\sqrt[3]{25}$,$\sqrt{x^2-x+1}$,$\sqrt{x^2-x}\ (x>1)$.
2. $x$是怎样的实数时，下列二次根式有意义？$(1)\dfrac{\sqrt{x+1}}{(x-3)^2}$, $(2) \dfrac{\sqrt{1-x}}{\sqrt{x-2}+1}$.
3. 已知实数$x,y,z$满足
   $$
   \sqrt{x+y-8}+\sqrt{8-x-y}=\sqrt{3x-y-z}+\sqrt{x-2y+z+3}
   $$
   求$x,y,z$.
4. 若化简$|1-x|-\sqrt{x^2-8x+16}$ 的结果为$2x-5$, 求$x$的取值范围.
5. 已知$y=\sqrt{2x-1}-\sqrt{1-2x}+8x$, 求$\sqrt{4x+5y-6}$的平方根_______.
6. 已知$a$是实数，求代数式$\sqrt{27-12a+2a^2}$的最小值.
7. 已知$\sqrt{1+x}-(y-1)\sqrt{1-y}=0$, 求$x^{2017}+y^{2017}$的值.
8. 已知$b\leq 0$, 化简$\sqrt{ab^3}$得_______.
9. 化简下列根式$(1)\ \sqrt{15}\times \dfrac{3}{5}\sqrt{20}\div (-\dfrac{1}{3}\sqrt6)$, $(2)\ \dfrac{\sqrt2}{\sqrt5-\sqrt2}$
10. 已知$x=\sqrt5+1,y=1-\sqrt5$, 试求代数式$x^3y^2+y^3x^2$的值.
11. 比较下列几组数的大小：$(1)-5\sqrt7$与$-4\sqrt{11}$, $(2)\ \sqrt2+\sqrt5$与
    $\sqrt{13}$, $(3)\ \sqrt{2019}-\sqrt{2018}$与$\sqrt{2017}-\sqrt{2016}$.
12. 计算
    $$
    \dfrac{1}{1+\sqrt2}+\dfrac{1}{\sqrt2+\sqrt3}+\dfrac{1}{\sqrt3+\sqrt4}+\cdots+\dfrac{1}{\sqrt{99}+\sqrt{100}}
    $$